Indigo-M: Induktionstomografie für Industrie, Gesundheitswesen und Objekterkennung - Mathematics

Problembeschreibung

Magnetische Induktionstomographie (MIT) ist ein bildgebendes Verfahren, das zurzeit noch Gegenstand der Forschung ist. MIT ist kostengünstig und harmlos für den Menschen, und könnte daher in Zukunft die etablierten bildgebenden Verfahren attraktiv ergänzen. 

MIT nutzt physikalische Effekte, die sich beim Zusammenspiel von elektrischen und magnetischen Feldern ergeben. Dabei bestimmt MIT die elektrische Leitfähigkeitsverteilung im Testkörper.

Die Herausforderung bei MIT liegt nicht zuletzt in der komplexen mathematischen Beschreibung, die sich aus den komplizierten Eigenschaften elektromagnetischer Felder ergeben.

An diesem Punkt setzt das Projekt INDIGO-M an: gezielter Einsatz mathematischer Methoden, die auf die Problemstellungen bei MIT zugeschnitten sind. Dabei werden klassische Modellierungen ebenso verwendet, wie die Nutzung von Methoden der Künstlichen Intelligenz durch Neuronale Netze.

Dabei ergeben sich, wie bei anderen Tomografie-Methoden auch, zwei wesentliche Probleme. Zum einen muss eine möglichst gute und schnelle Modellierung und Simulation der Beziehung σ→ Si, dem sog. Vorwärtsproblem gefunden und implementiert werden. Andererseits muss das inverse Problem Si→ σ gelöst werden.

Das inverse Problem bei MIT hat dabei im Vergleich zu anderen Methoden, wie etwa CT, eine spürbar höhere Komplexität. Dies liegt daran, dass sich bei jeder Signalmessung die Einflüsse aller zu bestimmenden Unbekannten überlagern, woraus sich eine maximale Kopplung der Unbekannten in den resultierenden Gleichungssystemen ergibt. Zudem ist der Zusammenhang Si→ σ nicht-linear und schlecht konditioniert.

Aus diesen Gründen hat das Projekt INDIGO-M das Ziel, für MIT innovative mathematische Ansätze zu entwickeln, um die oben genannten Probleme im Rahmen des grundsätzlich möglichen zu meistern.

Zurzeit beschränkt sich das Team dabei auf Leitfähigkeiten, wie sie im biomedizinischen Umfeld üblich sind (0 bis 1 S/m). Dies führt u.a. dazu, dass die Modellierung unter der Voraussetzung „weak-coupling“ im Sinne der Elektrodynamik möglich ist. Zudem erlauben die gewählte zeitharmonische Anregung und die Abmessungen des Aufbaus die Verwendung der Annahme „quasi-Magnetostatik“. Unter diesem Regime ist es dem Projektteam erfolgreich gelungen, wesentliche Fortschritte im Vorwärtsproblem, speziell bei der Verbesserung der Laufzeit, aber vor allem auch im inversen Problem zu erzielen (siehe Abschnitt Publikationen). Dabei kommen gleichermaßen klassische Methoden der Modellierung und numerischen Mathematik, wie auch neue Ansätze aus dem Bereich machine learning mit Neuronalen Netzen zum Einsatz.

  Ziele

• Verbesserung der Stabilität, Schärfe und Geschwindigkeit von MIT
• Promotionsvorhaben
• Publikationen
• Verstetigung des Forschungsthemas, u.a. durch Folgeprojekte
• Erhöhung des Bekanntheitsgrades der Technologie MIT
• Kooperationen mit anderen Forschungsgruppen

  Methoden

• Physikalische und mathematische Modellierung
• Numerische und abstrakte Mathematik
• Neuronale Netze (KI)

  Herausforderungen

• Nicht-linearer Zusammenhang zwischen Leitfähigkeitsverteilung und gemessenem Signal
• Schlecht konditioniertes inverses Problem
• Mathematisch optimales Design der Mess-Sensorik unter Berücksichtigung der technischen Realisierbarkeit

Status und Ergebnisse

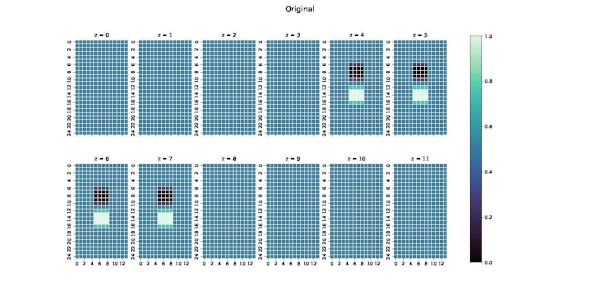
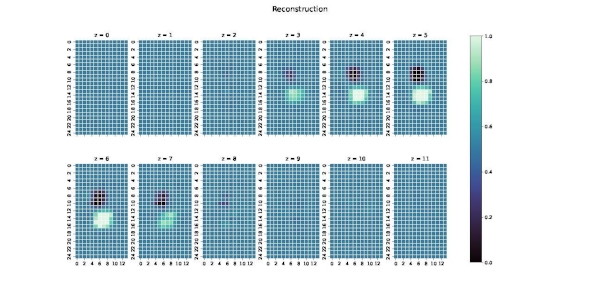
Im Vorwärtsproblem und im inversen Problem wird der Testkörper als quaderförmiges Volumen angenommen, dass durch ein cuboides rein resistives Netzwerk repräsentiert wird. Das ermöglicht es, die Modellierung der Wirbelströme J im Körper mittels Netzwerk-Theorie zu behandeln, sowohl im Sinne elektrischer Netzwerke im Rahmen der Elektrotechnik als auch von abstrakten Flüssen im Sinne der Graphen-Theorie.

Überhaupt hat sich die Unterteilung des Zusammenhangs σ↔S_i  in die Teilschritte σ↔J
und J↔S_i  als günstig erwiesen. Die bisher im Projekt etablierten Methoden lassen sich dabei wie folgt in einem Überblick zusammenfassen:

Vorwärtsproblem

σ→J:
1. klassische Knotenpotential-Methode (bekannt) 
2. Min-cost Flüsse mit quadratischer Kostenfunktion (bekannt)

J→S_i:
Lorentz-Reziprozität über das Vektorpotential der Empfänger-Spulen (bekannt)

Inverses Problem

σ←J:
1. Iteratives Verfahren (eigene Entwicklung, siehe [2])
2. Schnitte affiner Teilräume (eigene Entwicklung, siehe [3])

σ←S_i:
Neuronale Netze (eigene Entwicklung, siehe [1])

Die größte Herausforderung sieht das Projekt-Team zurzeit in der linearen, aber schlecht konditionierten Beziehung  J←S_i. An diesem Problem finden zurzeit intensive Forschungen statt, sowohl mit klassischen Methoden, z.B. Fourier-Analyse, als auch mittels machine learning.

Bezeichnet man mit A_i die Vektorpotentiale der Mess-Spulen, so kann man die oben erwähnte Lorentz-Reziprozität kurz in der Form S_i=A_i∙J schreiben. Dadurch ist die bisher problematische Beziehung J←S_i auf das engste verknüpft mit der Konstruktion optimaler Geometrien von Mess-Spulen. Hier kann sich Mathematik und Engineering optimal ergänzen, und es deuten sich derzeit weitere signifikante Fortschritte an. 

Publikationen

[1] Hofmann A, Klein M, Rueter D, Sauer A. A Deep Residual Neural Network for Image Reconstruction in Biomedical 3D Magnetic Induction Tomography. Sensors (Basel). 2022 Oct 18;22(20):7925. doi: 10.3390/s22207925. PMID: 36298274; PMCID: PMC9610508.
[2] Schledewitz T, Klein M, Rueter D. Magnetic Induction Tomography: Separation of the Ill-Posed and Non-Linear Inverse Problem into a Series of Isolated and Less Demanding Subproblems. Sensors (Basel). 2023 Jan 17;23(3):1059. doi: 10.3390/s23031059. PMID: 36772097; PMCID: PMC9920446.
[3] Wachs M, Primbs M. A new Solution to the Inverse Power Flow Problem in DC Networks using Affine Subspaces [Preprint submitted for publication].

  Zuordnung zum HRW-Leitthema

• Energie und Ressourcen
• Digitalisierung und Vernetzung
• Gesundheit und Versorgung